読み込めないACIS オブジェクトがあります。

他のCADで作成した3Dモデルを読み込む

ダイナモをお休みして、今回は他のCADシステムで作成した、3DモデルをRevitに取り込むときのちょっとしたコツをご紹介します。
下の図は3dsMAXのサンプルファイルです。これをRevitに取り込んでみます。

3dsMAXのサンプル「Ford Focus.max」

基本的にはDWGに変換してから読み込みます。Exportでファイル形式にDWGを指定して出力します。

AutoCAD DWGを指定して出力

Revitでファミリ、あるいはプロジェクトを開いて、「CADを読み込む」でこのデータを読み込んだ時に下の図のような警告が表示されます。

読み込めないACISオブジェクト？

一瞬どきりとしますが、この警告を回避するにはどうすればいいでしょう？

2007形式のDWGで読み込むとOK

回避方法は結構単純で、DWGの形式を2007形式(あるいは2004形式)にすることで、この警告はでなくなります。そればかりか読み込み時間もものすごく短くなります。

2007形式のDWGで読み込むと◎

ではなぜこのような違いがあるのでしょうか？最初の2013形式のファイルをAutoCADで開いて、プロパティを確認すると、「メッシュ」となっています。

オブジェクトは「メッシュ」

これはAutoCAD2010で登場したオブジェクトです。警告はこれを「ポリメッシュ」に変換しなさい、と言っているのです。AutoCADにメッシュをポリメッシュに変換するコマンドがあるのかというと、どうもこれはなさそうで、一番簡単な方法は、2007あるいは2004形式に保存することです。保存後のファイルを開いてオブジェクトをチェックしてみます。

メッシュがポリメッシュに変換されています。

確かに、「ポリメッシュ」に変換されています。Revitの「AutoCADを使ってポリメッシュオブジェクトに変換し・・・・」というのはこのことだったのです。
これをRevitに読み込むと、問題なく読み込めます。

読み込んだ3Dモデルの断面を表示するには？

3DモデルをRevitに読み込むときは、直接プロジェクトに読み込むのではなく、一旦ファミリに読み込んでから、そのファミリをプロジェクトにロードすると、断面を切ることができるようになります。下の図は、左はプロジェクトに直接DWGを読み込んだもので、右は同じDWGをファミリに読み込んでから、改めてプロジェクトにロードしたものです。見た目は何も変わりません。

左は直接DWGをプロジェクトに読み込んでいる

この車の断面図を作成してみます。

左：DWGをプロジェクトに直接読み込んだ場合 / 右：DWGをファミリに取り込んでプロジェクトにロードした場合

このように、プロジェクトにDWGを直接読み込むと、断面を切ることができません。一方、一旦DWGをファミリに取り込んでからロードした場合は、断面を作成することが可能です。

しかし、読み込み先のファミリのカテゴリには注意してください。一般モデルなど、切断可能なカテゴリを選べば断面は作成されますが、点景や家具など切断不可能なカテゴリを選んだ場合はやはり切断できません。

ダイナモ白熱教室(7)～点-線-面

前回作成したコサインカーブのZ座標をXY平面の座標に割り当ててみます。前回の最後のグラフは次のようになっていました。

このグラフでできたCosカーブをすべての座標に割り当てる

Point.Add / Vector.ByCoordinates

点にベクトルを与えて新しい点を作成するノードです。引数は

• point
• vectorToAdd

の二つで、pointは前々回に作成した、XY平面上(Z=0)の点のリストで、vectorToAddは前回のコサインカーブを基に新たに作成します。

VectorByCoordinatesのノードを追加し、下の図の水色の部分のようにZにつなぎます。

Zベクトルを作成

このベクトルを各点に割り当てます。まず、上図のピンク色のPoint.ByCoordenatesノードの右下の□をクリックし、リストを表示します。次にそのリストの最初の[0]Listを選択すると、背景の3Dビューに[0,0]などのインデックスが表示され、最初のリストがどこにあるのかを目視確認できます。

リストの所在が確認できる

この列に対して、コサインカーブを割り当てます。

List.Map

ベクトルを加算するリストは2次元配列になっています。この１次元側にZベクトルを加算します。この場合List.Mapを使い、各リストに処理をマッピングします。

• Point.Add
• List.Map

を追加し、次の図のように接続します。

List.Map

結果は下の図のようになります。

Y方向にコサインカーブを割り当て

List.Transpose

今度はX方向にコサインカーブを割り当ててみます。ピンク色の部分のPoint.ByCoordinatesからは[X,Y]のリストが出てくるので、これを反転して[Y,X]のリストにしてマップします。リストのX、Yを入れ替えるにはエクセルでもおなじみのTransposeノードを使用して、下の図のようにつなぎます。

Transpose

結果は・・・

X方向にコサインカーブを割り当て

NurbsCurve.ByPoint

この点を結んで曲線を作成し、さらに面を張ってみましょう。まずは

• NurbCurve.ByPoint

を追加し、List.Mapに接続します。すると、各リストがつながって曲線として表示されます。

NurbsCurve.ByPoints

Surface.ByLoft

曲線をつないで面を作成します。

• Surface.ByLoft

を追加し、NurbsCurve.ByPointsに接続すると、面が作成できます。

X方向にコサインカーブを割り当てた面の作成

Transposeを使わない最初のバージョンであれば

Y方向にコサインカーブを割り当てた面

ここでは「点」→「線」→「面」の基本的な流れを説明しました。

ダイナモ白熱教室(6)～Cos

前回は一定の割合で50m×20mのメッシュ状の点を作成しました。今回はZ方向にコサインカーブを描いてみます。

まずは単純にY=0の直線状にZ方向にコサインカーブで点を作成しましょう。

Math.Cosノード

Dynamoを立ち上げ、前回のファイルを開きます。

Numberノードを追加し「0..360..#res」とし、これをIntegerSlider(Resolution)と結びます。0°から360°をres分割したリストを作成します。

次にMath.CosノードとPoint.ByCoordinatesを追加し、下の図のように結ぶと、コサインカーブに沿った点が現れます。

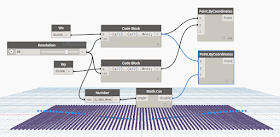振幅1.0のコサインカーブができた

振幅を可変化

cos(x)の最大値は１なので、これを任意の幅に書き換えれるようにします。また、(0,0)の位置で-1となるのでこれを反転するために負の値を掛けます。つまり

-Wz・Cos(a)

とします。

1. Number Sliderを追加し名前をWzとする。
2. *を二つとNumberを一つ追加し、Numberに-1を入力。
3. 下の図のようにつなぎます。

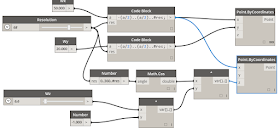-Wz・Cos (a)

Wzスライダーを動かして、コサインカーブの振幅幅が変化することを確認してください。

コサインカーブの変化を観察しよう！

次に、結果に振幅の値を加えることで、マイナスの値にならないようにします。

-Wz・Cos(a)+Wz

+ノードを追加して、次のように接続します。

コサインカーブがZ≧0にあることを確認してください。

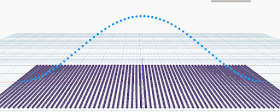全ての点がZ≧0に

周期を変更する

現状１周期ですが、これを3周期に変えてみます。式は周期をPeriodとして

-Wz・Cos(Period・a)+Wz

Numberノード、*ノードを追加し、下の図のように接続します。

3周期

Number Sliderで周期を可変化してもよいでしょう。

振幅に変化を加える

振幅が定数だと、周期ごとのカーブの形状は同じですが、振幅にもCosを割り当て変化を加えましょう。

f(a)=-Wz・Cos(a)+Wz

g(a)=-f(a)・Cos(Period・a)+f(a)

としてみましょう。こうのような関数のチェックにはGeoGebra（https://www.geogebra.org/)というアプリケーションが便利です。Windows Storeなどで入手できるので、チェックしてみてください。下の図はGeoGebraでこの関数を表示している様子です。

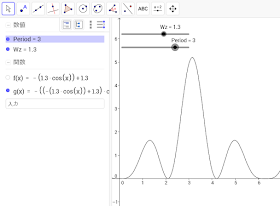GeoGebraは幾何学好きにはたまらない！

これをグラフに表わすと次のようになります。

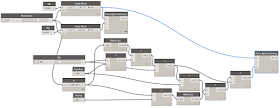ちょっと複雑になってきましたが・・

この結果は下の図のようになります。

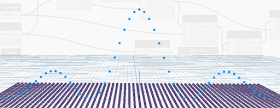振幅がCos

コードブロックでまとめる

コードブロックを使えば、もう少しグラフをわかりやすくすることができます。

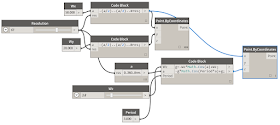コードブロックでスッキリ

このグラフでも同様の結果を得ることができます。コードブロックは適切に使えば、グラフをわかりやすくまとめることができます。ちょっとプログラマーっぽいですが、案外簡単に慣れてしまうものです。ぜひトライしてみてください。

ダイナモ白熱教室(5)～点

久しぶりにダイナモを取り上げます。先日ダイナモのサイトをみたところ、バージョンが0.8.1に上がっていましたので、これを使って話を進めます。

バージョン0.8.1が使えます

今回は大量の点をメッシュ状に作成し、これらをつないで面を作成するというプロセスを実験してみます。

原点を中心に50m×20mの点をつくってみる

原点(0,0,0)を中心としてX方向50m、Y方向20mの点を任意のピッチで作成してみます。

まず、Numberノードを2つ追加し、それぞれ名前をWx、Wyとし、値を50、20とします。

X座標は 最小値-25(-(50/2))から最大値25(50/2)です。さらにNumberノードを追加し、「min..max..#res」　(minからmaxの間をres分割した数字のリストを作成する）とすると、ノードの左側に変数として、min、max、resが並びます。

Numberノード

さらに「*」を２つ、「Number」を2つ、Integer Sliderを一つ追加します。二つのNumberノードを「0.5」「-0.5」とし、IntegerSliderの値を50程度にし、下の図のようにそれぞれを接続します。

Watchノードを終端のNumberノードに接続し、内容をチェックします。これがX座標のリストになります。

Watchノードでチェックする

Yについても同じことを繰り返します。0.5、-0.5、IntegerSliderはXY共通で使えます。＊２つと終端のNumberノードを選択し、コピーペーストして、Wyをつなぎなおします。

座標の作成

このXとYの座標リストを使って点を作成します。「Point.ByCoodinate」を追加し、XYをつなぎます。

バックグラウンドに座標が現れます。さらにPoint.Coordinatesノードを右クリックし、「レーシング」-「外積」を選びます。

IntegerSliderを動かして、変化を観察してください。

コードブロックを使ってみる

コードブロックを使えば、もう少しグラフをすっきりさせることができます。コードブロックはプログラムを記述するノードなのですが、リストを作成するぐらいであればだれでも気楽に使えます。

画面をダブルクリックすることで、コードブロックを作成します。そして、以下のように記述します。文末には必ず「;」が必要です。

-(a/2)..(a/2)..#res;

そして、既存の0.5、-0.5、*、式をかいたNumberノードを削除し、下の図のようにつなぐことで同じ結果を得ることができます。

コードブロックですっきり

次回はZ座標を加えてみます。